|
2.1 ΟΙ ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ (Επαναλήψεις - Συμπληρώσεις) Εισαγωγή Στο Γυμνάσιο μάθαμε ότι οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς και παριστάνονται με τα σημεία ενός άξονα, του άξονα των πραγματικών αριθμών.
Θυμίζουμε ότι:
Μπορούμε δηλαδή να πούμε ότι οι ρητοί αριθμοί αποτελούνται από τους δεκαδικούς και τους περιοδικούς δεκαδικούς αριθμούς.
Υπάρχουν όμως και αριθμοί, όπως οι |
|
Πράξεις Στους πραγματικούς αριθμούς ορίστηκαν οι πράξεις της πρόσθεσης και του πολλαπλασιασμού και, με τη βοήθειά τους, η αφαίρεση και η διαίρεση.
Στον πίνακα αυτόν, αλλά και στη συνέχεια του βιβλίου, τα γράμματα που χρησιμοποιούνται παριστάνουν οποιουσδήποτε πραγματικούς αριθμούς , εκτός αν δηλώνεται διαφορετικά. ΣΧΟΛΙΟ
Ομοίως, ένα γινόμενο με περισσότερους από δυο παράγοντες ισούται με οποιοδήποτε άλλο γινόμενο που μπορεί να σχηματισθεί από τους ίδιους αριθμούς με οποιαδήποτε σειρά και αν τους πάρουμε.
(Η απόδειξη των παραπάνω ισχυρισμών είναι αρκετά πολύπλοκη και παραλείπεται).
α - β = α + (-β) | ||||||||||||||||||
|
Δηλαδή: ΣΗΜΕΙΩΣΗ
1.
δηλαδή, δυο ισότητες μπορούμε να τις προσθέσουμε κατά μέλη. 2.
δηλαδή, δυο ισότητες μπορούμε να τις πολλαπλασιάσουμε κατά μέλη. 3.
δηλαδή, μπορούμε και στα δυο μέλη μιας ισότητας να προσθέσουμε ή να αφαιρέσουμε τον ίδιο αριθμό. 4.
δηλαδή, μπορούμε και τα δυο μέλη μιας ισότητας να τα πολλαπλασιάσουμε ή να τα διαιρέσουμε με τον ίδιο μη μηδενικό αριθμό. 5.
δηλαδή, το γινόμενο δύο πραγματικών αριθμών είναι ίσο με το μηδέν, αν και μόνο αν ένας τουλάχιστον από τους αριθμούς είναι ίσος με το μηδέν. α · β ≠ 0 ⇔ α ≠ 0 και β ≠ 0 |
|
ΣΧΟΛΙΟ α = 1 Όμως έχουμε και α = 1, οπότε το 1 θα είναι ίσο με το 0. Οδηγηθήκαμε στο λανθασμένο αυτό συμπέρασμα, διότι στην ισότητα (α + 1)(α - 1) = (α - 1) · 1 διαγράψαμε τον παράγοντα (α - 1) ο οποίος, λόγω της υπόθεσης, ήταν ίσος με μηδέν. |
|
Δυνάμεις Είναι γνωστή από το Γυμνάσιο η έννοια της δύναμης αριθμού με εκθέτη ακέραιο. Συγκεκριμένα, αν ο α είναι πραγματικός αριθμός και ο ν φυσικός, έχουμε ορίσει ότι: αν = α · α · α - α, για ν>1 και
Αν επιπλέον είναι α ≠ 0, τότε ορίσαμε ότι: α0 = 1 και ΣΧΟΛΙΟ
| |||||||||
|
Αξιοσημείωτες ταυτότητες Η έννοια της ταυτότητας είναι γνωστή από το Γυμνάσιο. Συγκεκριμένα, κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές των μεταβλητών αυτών λέγεται ταυτότητα.
|
|
Μέθοδοι απόδειξης 1η) Ευθεία Απόδειξη Έστω ότι για τρεις πραγματικούς αριθμούς α, β και γ ισχύει η συνθήκη α + β + γ = 0 και θέλουμε να αποδείξουμε ότι α3 + β3 + γ3 = 3αβγ, δηλαδή έστω ότι θέλουμε να αποδείξουμε τη συνεπαγωγή: « Αν α + β + γ = 0, τότε α3 + β3 + γ3 = 3αβγ ». Επειδή α + β + γ = 0, είναι α = -(β + γ) , οπότε θα έχουμε: ΣΧΟΛΙΑ (α2 + β2)(x2 + y2) = (αx + βy)2 + (αy - βx)2 Έχουμε διαδοχικά: |
|
3ο) Για να αποδείξουμε ότι ένας ισχυρισμός δεν είναι πάντα αληθής, αρκεί να βρούμε ένα παράδειγμα για το οποίο ο συγκεκριμένος ισχυρισμός δεν ισχύει ή, όπως λέμε, αρκεί να βρούμε ένα αντιπαράδειγμα. Έτσι ο ισχυρισμός «για κάθε α>0 ισχύει α2>α » δεν είναι αληθής, αφού για
2η) Μέθοδος της Απαγωγής σε Άτοπο «Αν ο α2 είναι άρτιος αριθμός, τότε και ο α είναι άρτιος αριθμός» Για την απόδειξη του ισχυρισμού αυτού σκεπτόμαστε ως εξής: = 4κ2 + 4κ + 1 =2(2κ2 + 2κ) + 1 = 2λ + 1 (όπου λ = 2κ2 + 2κ). Δηλαδή α2 = 2λ + 1, λ ∈ Ζ, που σημαίνει ότι ο α2 είναι περιττός. Αυτό όμως έρχεται σε αντίθεση με την υπόθεση ότι ο α2 είναι άρτιος. Επομένως, η παραδοχή ότι α δεν είναι άρτιος είναι λανθασμένη. Άρα ο α είναι άρτιος. Στην παραπάνω απόδειξη υποθέσαμε ότι δεν ισχύει αυτό που θέλαμε να αποδείξουμε και χρησιμοποιώντας αληθείς προτάσεις φθάσαμε σε ένα συμπέρασμα που έρχεται σε αντίθεση με αυτό που γνωρίζουμε ότι ισχύει. Οδηγηθήκαμε όπως λέμε σε άτοπο. |
|
ΕΦΑΡΜΟΓΕΣ 1η Να αποδειχθούν οι εξής ιδιότητες των αναλογιών: i) ii) iii) iv)
ΑΠΟΔΕΙΞΗ i) Για βδ ≠ 0 έχουμε: ii) Για βγδ ≠ 0 έχουμε:
iii) Για βδ ≠ 0 έχουμε: iν) Για βδ (β + δ) ≠ 0, αν θέσουμε 2η Να αποδειχθεί ότι ο αριθμός
|
|
ΑΠΟΔΕΙΞΗ Έστω ότι ο
που σημαίνει ότι ο κ2 είναι άρτιος, οπότε (σελ. 25) και ο κ είναι άρτιος, δηλαδή είναι της μορφής
κ = 2μ. κ2 = 2λ2 Που σημαίνει ότι ο λ2 είναι άρτιος, άρα και ο λ είναι άρτιος.
Στο σημείο Α του πραγματικού άξονα που παριστάνει τον αριθμό 1 υψώνουμε κάθετο τμήμα ΑΒ με μήκος 1. Τότε η υποτείνουσα του ορθογωνίου τριγώνου ΟΑΒ έχει μήκος ίσο με
|
|
Ασκήσεις
|
|||||||||||||||||||||||||||||||||||
|
2.2 ΔΙΑΤΑΞΗ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ Έννοια της διάταξης Οι έννοιες «μεγαλύτερος από», «μικρότερος από», που είναι γνωστές από το Γυμνάσιο, ορίστηκαν ως εξής:
Έτσι ο αρχικός ορισμός γράφεται ισοδύναμα: α > β ⇔ α - β > 0 Γεωμετρικά η ανισότητα α > β σημαίνει ότι, πάνω στον άξονα των πραγματικών ο αριθμός α είναι δεξιότερα από τον β .
Αν για τους αριθμούς α και β ισχύει α > β ή α = β , τότε γράφουμε α ≥ β και διαβάζουμε: «α μεγαλύτερος ή ίσος του β». |
Από την τελευταία εύκολα προκύπτουν και οι ισοδυναμίες: α2 + β2 = 0 ⇔ α = 0 και β = 0 α2 + β2 > 0 ⇔ α ≠ 0 ή β ≠ 0 |
|
Ιδιότητες των ανισοτήτων Στηριζόμενοι στην ισοδυναμία α > β ⇔ α - β > 0, μπορούμε να αποδείξουμε τις παρακάτω ιδιότητες των ανισοτήτων: 1.
2.
3.
Η ιδιότητα 3. ισχύει και για περισσότερες ανισότητες. Συγκεκριμένα:
Στη συνέχεια θα αποδείξουμε και την παρακάτω ιδιότητα. |
|
4.
ΑΠΟΔΕΙΞΗ
α1 = α2 = ... = αν = α > 0 και β1 = β2 = ... = βν = β > 0, προκύπτει ότι: αν > βν.
Με τη βοήθεια της παραπάνω ιδιότητας θα αποδείξουμε τώρα ότι: Για θετικούς αριθμούς α, β και θετικό ακέραιο ν ισχύει η ισοδυναμία: α = β ⇔αν = βν |
|
ΑΠΟΔΕΙΞΗ
Άρα, α = β. |
|
ΣΧΟΛΙΑ 1ο Σύμφωνα με την ιδιότητα 3, αν δυο ανισότητες της ίδιας φοράς τις προσθέσουμε κατά μέλη, προκύπτει ανισότητα της ίδιας φοράς. Δεν συμβαίνει όμως το ίδιο με την αφαίρεση. Για παράδειγμα, είναι 10 > 6 και 7 > 2, αλλά 10 - 7 < 6 - 2 . 2ο Επίσης, σύμφωνα με την ιδιότητα 3, αν δυο ανισότητες της ίδιας φοράς με θετικούς, όμως, όρους τις πολλαπλασιάσουμε κατά μέλη, προκύπτει ανισότητα της ίδιας φοράς. Δεν συμβαίνει όμως το ίδιο με τη διαίρεση. Για παράδειγμα, είναι 24 > 10 και 6 > 2, αλλά
|
|
Διαστήματα Το σύνολο των πραγματικών αριθμών x με α ≤ x ≤ β λέγεται κλειστό διάστημα από α μέχρι β και συμβολίζεται με [α, β].
Τέλος, υπό μορφή διαστήματος,
Με ανάλογο τρόπο ορίζονται και τα διαστήματα (α, +∞) και (-∞, α). Τα σύμβολα +∞ και -∞, που διαβάζονται «συν άπειρο» και «πλην άπειρο» αντιστοίχως, δεν παριστάνουν πραγματικούς αριθμούς. |
|
|
ΕΦΑΡΜΟΓΕΣ 1η Να αποδειχθεί ότι : i) Αν α, β ομόσημοι αριθμοί, τότε
ii) Για όλους τους πραγματικούς αριθμούς α, β ισχύει α2 + β2 ≥ 2αβ iii) Αν α>0, τότε
ΑΠΟΔΕΙΞΗ i) Αφού α, β είναι ομόσημοι αριθμοί έχουμε αβ>0 . Επομένως ισχύει:
ii) Έχουμε: α2 + β2 ≥ 2αβ ⇔α2 + β2 - 2αβ ≥ 0 ⇔ (α - β)2 ≥ 0, που ισχύει iii) Έχουμε: |
|
2η Αν
-11 < 8x -12y + 3 < 17 ΑΠΟΔΕΙΞΗ Από την ανισότητα
Ομοίως από την
Προσθέτουμε τώρα κατά μέλη τις ανισότητες (1) και (2), που έχουν την ίδια φορά, και έχουμε: -14<8x -12y<14, οπότε θα ισχύει: -14 + 3<8x -12y + 3<14 + 3 Άρα -11<8x -12y + 3<17 |
|
Ασκήσεις
|
||||||||||||||||||||||||||
|
2.3 ΑΠΟΛΥΤΗ ΤΙΜΗ ΠΡΑΓΜΑΤΙΚΟΥ ΑΡΙΘΜΟΥ Ορισμός της απόλυτης τιμής Θεωρούμε έναν αριθμό α που παριστάνεται με το σημείο Α πάνω σε έναν άξονα.
Γνωρίζουμε από το Γυμνάσιο ότι η απόσταση του σημείου Α από την αρχή Ο, δηλαδή το μήκος του ευθύγραμμου τμήματος ΟΑ, ονομάζεται απόλυτη τιμή του αριθμού α και συμβολίζεται με |α|. •
• |0| = 0 |
Από τα προηγούμενα συμπεραίνουμε αμέσως ότι:
Για παράδειγμα,
|
|
Ιδιότητες των απόλυτων τιμών Από τον τρόπο εκτέλεσης των πράξεων μεταξύ πραγματικών αριθμών, προκύπτουν για τις απόλυτες τιμές οι ακόλουθες ιδιότητες:
Οι ιδιότητες αυτές, όμως, μπορούν να αποδειχθούν και με τη βοήθεια των προηγούμενων συμπερασμάτων. ΑΠΟΔΕΙΞΗ 1. Επειδή και τα δύο μέλη της ισότητας |α · β| = |α| · |β| είναι μη αρνητικοί αριθμοί, έχουμε διαδοχικά: 2. Αποδεικνύεται με τον ίδιο τρόπο. 3. Επειδή και τα δύο μέλη της ανισότητας |α + β|≤|α| + |β| είναι μη αρνητικοί αριθμοί, έχουμε διαδοχικά: Είναι φανερό ότι η ισότητα αβ = |αβ| ισχύει αν και μόνο αν αβ ≥ 0 , δηλαδή αν και μόνο αν οι αριθμοί α και β είναι ομόσημοι ή ένας τουλάχιστον από αυτούς είναι ίσος με μηδέν. ΣΧΟΛΙΟ
|α1 · α2 · ... · αν| = |α1| · |α2| · ... · |αν| Στην ειδική μάλιστα περίπτωση που είναι α1 = α2 = ... = αν = α, έχουμε:|αν| = |α|ν
Συγκεκριμένα: |α1 + α2 + ... + αν| ≤ |α1| + |α2| + ... + |αν| |
|
Απόσταση δυο αριθμών
Το μήκος του τμήματος ΑΒ λέγεται απόσταση των αριθμών -2 και 3. Παρατηρούμε ότι
(ΑΒ ) = 5 = |(-2) - 3| = |3 - (-2)|.
Το μήκος του τμήματος ΑΒ λέγεται απόσταση των αριθμών α και β, συμβολίζεται με d(α,β) και είναι ίση με |α- β|. Είναι δηλαδή:
Προφανώς ισχύει d (α, β) = d (β, α) . Στην περίπτωση μάλιστα που είναι α<β, τότε η απόσταση των α και β είναι ίση με β - α και λέγεται μήκος του διαστήματος [α, β].
Αν Μ (x0) είναι το μέσον του τμήματος AB, τότε έχουμε (MA) = (MB) ⇔d(x0, α) = d(x0, β)⇔|x0 - α| = |x0 - β| ⇔x0 - α = β - x0, (αφού α< x0 <β) ⇔2x0 = α + β ⇔ 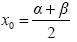
|
|
Ο αριθμός
Ως μήκος, κέντρο και ακτίνα των διαστημάτων (α, β), [α, β) και (α, β] ορίζουμε το μήκος, το κέντρο και την ακτίνα του διαστήματος [α, β].
Από τον ορισμό της απόστασης έχουμε: Γενικά:
Δηλαδή, οι αριθμοί x που ικανοποιούν τη σχέση |x -x0|<ρ είναι τα σημεία του διαστήματος (x0 - ρ, x0 + ρ) που έχει κέντρο το x0 και ακτίνα ρ.
Στην ειδική περίπτωση που είναι x0 = 0 , έχουμε: |x|<ρ ⇔x ∈(-ρ, ρ) ⇔-ρ<x<ρ . Για παράδειγμα,|x|<2 ⇔x ∈(-2, 2) ⇔-2<x<2 . • Έστω, τώρα, ότι θέλουμε να βρούμε τους πραγματικούς αριθμούς x για τους οποίους ισχύει |x - 3|>2.
Από τον ορισμό της απόστασης έχουμε: |x - 3|>2⇔d (x,3)>2⇔x < 3 - 2 ή x > 3 + 2 ⇔x ∈ (-∞, 3 - 2)∪(3 + 2, +∞). |
|
Γενικά:
Δηλαδή οι αριθμοί x που ικανοποιούν τη σχέση |x - x0|>ρ αντιστοιχούν σε σημεία Μ(x) του άξονα x΄x που απέχουν από το σημείο Κ(x0) απόσταση μεγαλύτερη του ρ.
Στην ειδική περίπτωση που είναι x0 = 0 , η τελευταία ισοδυναμία παίρνει τη μορφή: |x|>ρ ⇔x<-ρ ή x>ρ Για παράδειγμα: |x|>2 ⇔x<-2 ή x>2 . |
|
Ασκήσεις
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Τετραγωνική ρίζα μη αρνητικού αριθμού Στο Γυμνάσιο μάθαμε την έννοια της τετραγωνικής ρίζας μη αρνητικού αριθμού και τις ιδιότητές της. Συγκεκριμένα μάθαμε ότι: ΟΡΙΣΜΟΣ
Μπορούμε επομένως να πούμε ότι: Για τις τετραγωνικές ρίζες μη αρνητικών αριθμών γνωρίσαμε τις παρακάτω ιδιότητες:
|
|
ν-οστή ρίζα μη αρνητικού αριθμού
Ο αριθμός 4 λέγεται τρίτη ρίζα του 64 και συμβολίζεται με |
|
ΟΡΙΣΜΟΣ
|
|
Επίσης γράφουμε
Μπορούμε επομένως να πούμε ότι: ΣΧΟΛΙΟ (1)Αποδεικνύεται ότι υπάρχει και είναι μοναδικός |
|
Ιδιότητες των ριζών Από τον ορισμό της ν-οστής ρίζας ενός μη αρνητικού αριθμού α , συμπεραίνουμε αμέσως ότι:
Για παράδειγμα:
Ισχύουν όμως και οι ακόλουθες ιδιότητες, από τις οποίες οι δύο πρώτες είναι ανάλογες των ιδιοτήτων της τετραγωνικής ρίζας:
ΑΠΟΔΕΙΞΗ
2. Αποδεικνύεται όπως και η 1. 3. Έχουμε:
4. Έχουμε:
|
|
ΣΧΟΛΙΟ
|
|
Δυνάμεις με ρητό εκθέτη Στη συνέχεια θα ορίσουμε παραστάσεις της μορφής |
|
ΟΡΙΣΜΟΣ
Επιπλέον, αν μ, ν θετικοί ακέραιοι, τότε ορίζουμε Με τη βοήθεια των ιδιοτήτων των ριζών αποδεικνύεται ότι οι ιδιότητες των δυνάμεων με ακέραιο εκθέτη ισχύουν και για δυνάμεις με ρητό εκθέτη. Το γεγονός αυτό διευκολύνει το λογισμό με τα ριζικά. Έτσι έχουμε για παράδειγμα είναι:
|
|
ΕΦΑΡΜΟΓΕΣ 1η Αν α και β είναι μη αρνητικοί αριθμοί, να αποδειχθεί η ισοδυναμία:
ΑΠΟΔΕΙΞΗ Έχουμε: 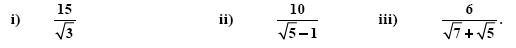 ΛΥΣΗ Έχουμε: 3η Να αποδειχθεί ότι:
ΑΠΟΔΕΙΞΗ Έχουμε: |
|
Ασκήσεις
|
||||||||||||||||||||||||||||||||||||
|
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ 1ου ΚΕΦΑΛΑΙΟΥ
|
|
ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ
| ||||